Stacks and Queues

STACK

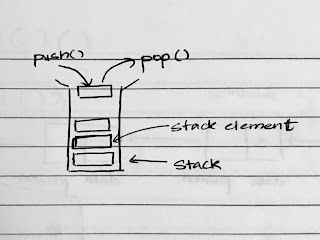
A stack is a linear data structure that only allows operations on the last added element in the stack. A stack can be visualized as a jar that is open from the top, so you can only put stuff or take out stuff from the top.

Stacks are almost always with two basic operations - push and pop.
Push inserts a new element in the stack from the top and Pop takes out the element at the top of the stack. Stacks follow LIFO order (Last In First Out).

A stack can be implemented using array or linked list.

Top in stack is the element at the top of the stack.

In C++, we can use the Standard Template Library implementation of Stack as: 

 #include <iostream>  
 #include <stack>  
 using namespace std;  
 int main()  
 {  
      stack <int> x;  
      x.push(1);  
      x.push(2);  
      x.push(4);  
      cout<<x.top()<<endl; // 4 is at top  
      x.pop(); // pops 4  
      x.pop(); // pops 2  
      cout<<x.top()<<endl; // 1 is at top  
      return 1;  
 }  

Stack Implementation using array :

 #include <iostream>   
  using namespace std;   
  // This is implementation of stack of size 10   
  struct stack{   
    int top = -1;   
    void push(int val)   
    {      
       if(top<9)   
       { top = top + 1;   
       cout<<"top after push: "<<top<<" -> value : "<<val<<endl;    
       arr[top] = val; }   
       else   
       { cout<<"Stack Overflow, could not insert "<<val<<" in stack"<<endl; }   
    }   
    int pop()   
    {   
       if(top<0) { cout<<"Stack Underflow"; return 0; }   
       int x = arr[top];   
       top = top - 1;    
       return x;   
    }   
    int arr[10]; // maximum size for stack is 100   
  };   
  int main()   
  {   
    struct stack x;   
    x.push(1);   
    x.push(2);   
    x.push(3);   
    x.push(4);   
    x.push(5);   
    x.push(6);   
    x.push(7);   
    x.push(8);   
    x.push(9);   
    x.push(10);   
    x.push(20);   
    x.push(30);   
    cout<<"Value popped out : "<<x.pop()<<endl;  
    cout<<"Value popped out : "<<x.pop()<<endl;  
    cout<<"Value popped out : "<<x.pop()<<endl;   
  }  

Output :

QUEUE

Queue is another linear data structure that is similar to stack but it removes the element that was inserted earliest and follows FIFO order (First In First Out).

In stack, we just needed to keep track of one index top but in Queue, we need to keep track of two indices front and rear. In Queue, insertion is Enqueue and deletion is Dequeue. Enqueue is done at rear and Dequeue from front. 

Implementation of queue of size 10 using array :

 #include <iostream>  
 using namespace std;  
 // This is implementation of queue of size 10  
 struct queue{  
      int front = 0;  
      int rear = 9;  
      int array[10];  
      int size = 0;  
      void enqueue(int val){  
                     if(size == 10) { return; }  
                     rear = (rear+1) % 10;  
                     array[rear] = val;  
                     size = size + 1 ;  
                     cout<<"Rear after enqueue : "<<rear<<endl;  
      }  
      int dequeue(){  
                if(size == 0) { return 0; }  
                int x = array[front];  
                front = (front+1) % 10;  
                size = size - 1 ;  
                cout<<"Front after dequeue : "<<front<<endl;   
                return x;  
      }  
 };  
 int main()  
 {       
      struct queue x;  
      x.enqueue(1);  
      x.enqueue(10);  
      x.enqueue(20);  
      x.enqueue(30);  
      x.enqueue(40);  
      x.enqueue(50);  
      x.enqueue(1);  
      x.dequeue();  
      x.dequeue();  
      x.dequeue();  
      x.enqueue(20);  
      x.enqueue(30);  
      x.dequeue();  
      x.dequeue();  
      x.dequeue();  
      x.dequeue();  
      return 0;  
 }  

Output : 

We increase front and rear in circular order by dividing by capacity and taking the remainder.